排序算法

排序算法

冒泡排序

思路：遍历第 0 个元素到第 n - 1 个元素，比较第i个元素与第i+1个元素，每轮遍历都能将最小（大）元素放至头（尾），这个过程就像冒泡一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从小到大原地排序
// 1: 3, 38, 5, 44, 15, 36, 26, 27, 2, 46, 4, 19, 47, 48, 50
// 2: 3, 5, 38, 15, 36, 26, 27, 2, 44, 4, 19, 46, 47, 48, 50
// 3: 3, 5, 15, 36, 26, 27, 2, 38, 4, 19, 44, 46, 47, 48, 50
// 4: 3, 5, 15, 26, 27, 2, 36, 4, 19, 38, 44, 46, 47, 48, 50
// 5: 3, 5, 15, 26, 2, 27, 4, 19, 36, 38, 44, 46, 47, 48, 50
// 6: 3, 5, 15, 2, 26, 4, 19, 27, 36, 38, 44, 46, 47, 48, 50
// 7: 3, 5, 2, 15, 4, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50
// 8: 3, 2, 5, 4, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50
// 9: 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50
for(int i = 0; i < n - 1; i++)
{
	for(int j = 0; j < n - i - 1; j++)
	{
		if(nums[j] > nums[j + 1])
		{
			swap(nums[j], nums[j + 1]);
		}
	}
}

最快的情况是已有序，最慢的情况是逆序，平均时间复杂度是O(n2)，是一种稳定的排序算法

可优化的做法是通过flag判断是否已经有序，有序时则可早退

选择排序

思路：每次遍历在未排序序列中选出最小（大）的数放置到已排序序列的末尾

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从小到大原地排序
// 1: 2, 44, 38, 5, 47, 15, 36, 26, 27, 3, 46, 4, 19, 50, 48
// 2: 2, 3, 38, 5, 47, 15, 36, 26, 27, 44, 46, 4, 19, 50, 48
// 3: 2, 3, 4, 5, 47, 15, 36, 26, 27, 44, 46, 38, 19, 50, 48
// 4: 2, 3, 4, 5, 47, 15, 36, 26, 27, 44, 46, 38, 19, 50, 48
// 5: 2, 3, 4, 5, 15, 47, 36, 26, 27, 44, 46, 38, 19, 50, 48
// 6: 2, 3, 4, 5, 15, 19, 36, 26, 27, 44, 46, 38, 47, 50, 48
// 7: 2, 3, 4, 5, 15, 19, 26, 36, 27, 44, 46, 38, 47, 50, 48
// 8: 2, 3, 4, 5, 15, 19, 26, 27, 36, 44, 46, 38, 47, 50, 48
// 9: 2, 3, 4, 5, 15, 19, 26, 27, 36, 44, 46, 38, 47, 50, 48
// 10: 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 46, 44, 47, 50, 48
// 11: 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48
// 12: 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48
// 13: 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 50, 48
// 14: 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50
for(int i = 0; i < n - 1; i++)
{
	int mmin = i;
	for(int j = i + 1; j < n; j++)
	{
		if(nums[mmin], nums[j]);
			mmin = j;
	}
	swap(nums[mmin], nums[i]);
}

时间复杂度为O(n2)，选择排序并不稳定，如[3, 5, 5, 4]，就会改变两个5的相对位置。适用于小型数据集排序

插入排序

思路：分为未排序序列和已排序序列，将未排列序列逐一插入到已排序序列中的相应位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从小到大原地排序
vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();
for(int i = 1; i < n; i ++)
{
	int target = nums[i];
	for(int j = i - 1; j >= 0; j--)
	{
        if(nums[j] > target)
        {
            nums[j + 1] = nums[j];
        }
        else
        {
            nums[j + 1] = target;
            break;
        }
	}
}

时间复杂度为O(n2)，不需要额外内存来存储中间结果，是稳定的排序算法。适用于规模较小的排序序列

希尔排序

也称递减增量排序，将序列分成更小的序列，然后对小序列使用插入排序，从而减小排序列表交换次数。非稳定排序

首先定义一个增量序列的整数序列，用于确定子序列大小，最常用的增量序列是Knuth序列

1
2
int h = 1;
while(h < n) h = 3 * h + 1;

以增量序列为步长，从最大增量开始，向下迭代到最小增量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从小到大原地排序
vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();
while(h >= 1)
{
	for(int i = h; i < n; i++)
	{
		for(int j = i; j >= h && nums[j] < nums[j - h]; j -= h)
		{
			swap(nums[j], nums[j - h]);
		}
	}
	
	h = h / 3;
}

归并排序

思路：基于分而治之的思想，将序列不断细分，细分成只有一个或两个元素的子序列，排序好后再合并回原来规模的序列。不需要交换比较，需要创建一个临时数组保存结果

递归法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从小到大排序

void merge(vector<int>& nums, int st, int mid, int en)
{
	vector<int> tmp(en - st + 1);
	int i = st, j = mid + 1;
	int k = 0;
	
	while(i <= mid && j <= en)
	{
		if(nums[i] < nums[j])
			tmp[k++] = nums[i++];
		else
			tmp[k++] = nums[j++];
	}
	
	while(i <= mid)
	{
		tmp[k++] = nums[i++];
	}
	
	while(j <= en)
	{
		tmp[k++] = nums[j++];
	}
	
	for(int m = st, n = 0; m <= en; m++, n++)
	{
		nums[m] = tmp[n];
	}
}

void merge_sort(vector<int>& nums, int st, int en)
{
	if(st == en)
		return;
	int mid = st + (en - st) / 2; // 计算中点，防止溢出
	merge_sort(nums, st, mid);
	merge_sort(nums, mid + 1, en);
	merge(nums, st, mid, en);
}

vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();
merge_sort(nums, 0, n - 1);

优化1：用不同方法处理小规模问题，减少函数调用次数：在小数组上用插入排序，if(en - st <= 10){Insert_sort(vector<int>& nums, int st, int en);}

优化2：剪枝，在合并前先判断两个子序列是否已经有序，即nums[st] < ... < nums[mid] < ... < nums[en]

时间复杂度为O(nlogn)，空间复杂度为O(n)

迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void merge_sort(vector<int>& nums) {
    int n = nums.size();

    // 从子数组大小为1开始，逐步翻倍
    for (int curr_size = 1; curr_size <= n - 1; curr_size *= 2) {
        // 遍历整个数组，合并相邻的子数组
        for (int left_start = 0; left_start < n - 1; left_start += 2 * curr_size) {
            // 计算中点和右边界
            int mid = min(left_start + curr_size - 1, n - 1);
            int right_end = min(left_start + 2 * curr_size - 1, n - 1);

            // 合并两个子数组
            merge(nums, left_start, mid, right_end);
        }
    }
}

时间复杂度是O(nlogn)，避免了递归调用产生的栈空间消耗，适用于处理大规模数据，特别是可以通过并行化加快排序过程。归并排序是稳定排序

快速排序

思路：选出一个元素称为基准元素，将所有比基准值小的移动到基准左边，比基准值大的移动到右边，最后递归地把两边的子序列排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从小到大排序

int partition(vector<int>& nums, int st, int en)
{
	int pivot = nums[st];
	
	while(st < en)
	{
		while(st < en && nums[en] >= pivot)
		{
			en--;
		}
		nums[st] = nums[en];
		while(st < en && nums[st] <= pivot)
		{
			st++;
		}
		nums[en] = nums[st];
	}
	nums[st] = pivot;
	return st;
}

void quick_sort(vector<int>& nums, int st, int en)
{
	if(st > en)
		return;
	int pivot = partition(nums, st, en);
	quick_sort(nums, st, pivot - 1);
	quick_sort(nums, pivot + 1, en);
}

vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();
quick_sort(nums, 0, n - 1);

时间复杂度O(nlogn)，就地排序，容易并行化

堆排序

先创建一个堆，不断把堆首元素与堆尾互换，再调整堆，保证堆首的一直都是未排序的最大值，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从大到小原地排序,建立一个小根堆，因为小根堆不断将当前最小值放到堆尾
void adjustify(vector<int>& nums, int i, int n)
{
	int l = 2 * i + 1, r= 2 * i + 2;
	int mmin = i;
	if(l <=n && nums[l] < nums[mmin])
	{
		mmin = l;
	}
	if(r <= n && nums[r] < nums[mmin])
	{
		mmin = r;
	}
	if(mmin != i)
	{
		swap(nums[i], nums[mmin]);
		adjustify(nums, mmin, n);
	}
}

vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();

// 构建堆
for(int i = n / 2; i >= 0; i--)
{
	adjustify(nums, i, n - 1);
}

// 堆排序
for(int i = n - 1; i > 0; i--)
{
	swap(nums[i], nums[0]);
	adjustify(nums, 0, i - 1);
}
reverse(nums.begin(), nums.end());

堆排序的平均时间复杂度为 Ο(nlogn)

计数排序

当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 Θ(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法

思路：找出待排序数组中的最大和最小元素，创建大小为 k=max−min+1的计数数组，记录数组中每个元素值出现次数，反向填充目标数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从大到小原地排序,建立一个小根堆，因为小根堆不断将当前最小值放到堆尾
void adjustify(vector<int>& nums, int i, int n)
{
	int l = 2 * i + 1, r= 2 * i + 2;
	int mmin = i;
	if(l <=n && nums[l] < nums[mmin])
	{
		mmin = l;
	}
	if(r <= n && nums[r] < nums[mmin])
	{
		mmin = r;
	}
	if(mmin != i)
	{
		swap(nums[i], nums[mmin]);
		adjustify(nums, mmin, n);
	}
}

vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();

// 1. 找到最大值和最小值
    int max_val = nums[0];
    int min_val = nums[0];
    for (const auto& num : nums) {
        if (num > max_val) max_val = num;
        if (num < min_val) min_val = num;
    }

    int range = max_val - min_val + 1;

    // 2. 创建计数数组并初始化为0
    vector<int> count(range, 0);

    // 3. 统计每个元素的出现次数
    for (const auto& num : nums) {
        count[num - min_val]++;
    }

    // 4. 修改计数数组为前缀和数组
    for (int i = 1; i < count.size(); ++i) {
        count[i] += count[i - 1];
    }

    // 5. 输出数组，并保持稳定性
    vector<int> output(nums.size());
    // 从后向前遍历原数组，以保持稳定性
    for (int i = nums.size() - 1; i >= 0; --i) {
        output[count[nums[i] - min_val] - 1] = nums[i];
        count[nums[i] - min_val]--;
    }
    
    nums = output;

时间复杂度：O(n+k)，其中 n 是数组的长度，k 是元素的范围。空间复杂度：O(k+n)，需要额外的计数数组和输出数组。

从后向前遍历原数组，确保排序的稳定性,适用于元素范围较小的情况

桶排序

桶排序是计数排序的改进版，利用函数映射关系与桶对应，而不是根据元素大小开辟数组

思路：设定定量的数组当空桶，遍历序列一一放置到对应的桶中，对非空桶进行排序，最后放置回原数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// nums = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}, 按从大到小原地排序,建立一个小根堆，因为小根堆不断将当前最小值放到堆尾
void adjustify(vector<int>& nums, int i, int n)
{
	int l = 2 * i + 1, r= 2 * i + 2;
	int mmin = i;
	if(l <=n && nums[l] < nums[mmin])
	{
		mmin = l;
	}
	if(r <= n && nums[r] < nums[mmin])
	{
		mmin = r;
	}
	if(mmin != i)
	{
		swap(nums[i], nums[mmin]);
		adjustify(nums, mmin, n);
	}
}

vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();

vector<vector<int>> buckets(n);
for(int i = 0; i < n; i++)
{
	int bucket_ind = nums[i] / n;
	buckets[bucket_ind].push_back(nums[i]);
}

for(int i = 0; i < n; i++)
{
	sort(buckets[i].begin(), buckets[i].end());
}

int idx = 0;
for(int i = 0; i < n; i++)
{
	for(int j = 0; j < buckets[i].size(); j++)
	{
		nums[idx++] = buckets[i][j];
	}
}

桶排序的平均时间复杂度是 O(n+k)，其中 n 是元素个数，k 是桶的数量。如果元素均匀分布，排序时间为O(n)，最坏情况下，所有元素落入一个桶中，时间复杂度退化为O(nlogn)

基数排序

思路：将整数按位数切割成不同的数字，然后按每个位数分别比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// 获取数组中最大元素的位数
int getMaxDigits(const vector<int>& nums) {
    int max_num = nums[0];
    for (const auto& num : nums) {
        if (num > max_num)
            max_num = num;
    }
    int digits = 0;
    while (max_num > 0) {
        digits++;
        max_num /= 10;
    }
    return digits;
}
vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();


int max_digits = getMaxDigits(nums);
int exp = 1; // 当前处理的位数，1 表示个位，10 表示十位，依此类推

// 使用计数排序作为子过程，对每一位进行排序
for (int d = 0; d < max_digits; d++) {
    int n = nums.size();
    vector<int> output(n);
    int count[10] = {0};

    // 统计当前位上每个数字出现的次数
    for (int i = 0; i < n; i++) {
    	int digit = (nums[i] / exp) % 10;
    	count[digit]++;
    }

    // 将 count 修改为前缀和数组，表示当前位上小于等于该数字的总数
    for (int i = 1; i < 10; i++) {
    	count[i] += count[i - 1];
    }

    // 从后向前遍历数组，确保排序的稳定性
    for (int i = n - 1; i >= 0; i--) {
        int digit = (nums[i] / exp) % 10;
        output[count[digit] - 1] = nums[i];
        count[digit]--;
    }

    // 将排序结果复制回原数组
    for (int i = 0; i < n; i++) {
    	nums[i] = output[i];
    }

    // 处理下一位
    exp *= 10;
}

位图排序

思路：根据待排序序列中最大的数，开辟一个数组或用bitset表示，每一位表示对应整数出现的次数

只需要遍历一次就能完成排序，输出排序后的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<int>nums{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
int n = nums.size();

bitset<N> bits;
for(int i = 0; i < n; i++)
{
	bits.set(i, 1);
}

for(int i = 0; i < n; i++)
{
	if(bits[i] == 1)
		cout << i << " ";
}

适用场景：不重复的序列，快速判断一个数是否出现在序列当中，或者判断一个数是否会重复出现。用作排序，需要知道序列在一个大概的范围当中

总结

img

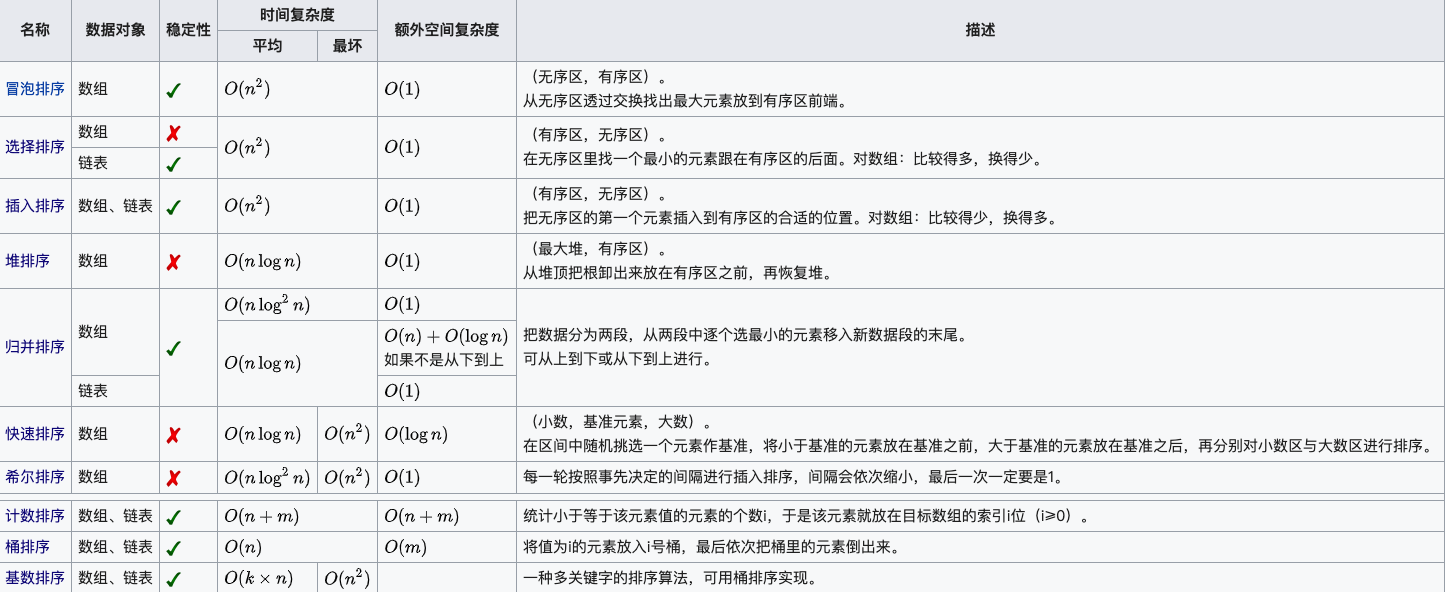
基于非比较的算法：计数排序、桶排序、基数排序，通常非比较的算法时间复杂度会更快， 基于比较的算法时间复杂度上限是O(nlogn)

就地排序算法：冒泡排序、选择排序、插入排序、对排序、希尔排序

稳定排序算法：冒泡排序、插入排序、归并排序、基数排序

非稳定排序算法：选择排序、快速排序、希尔排序、堆排序

外部排序算法：归并排序、基数排序、堆排序、桶排序

注

C++中的std::sort

std::sort的底层实现原理是introspective Sort内省排序实现，结合了快排、堆排和插入排序的优点

std::sort的具体步骤：对整个数组进行快速排序 ，当快排的递归深度超过log(n)时，就会切换到堆排序，避免了快排的最坏情况下的性能问题，当子数组的规模较小时，使用插入排序来提高性能

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <algorithm>
#include <vector>
#include <iostream>

// 快速排序的分区函数
template<typename Iterator, typename Compare>
Iterator partition(Iterator first, Iterator last, Compare comp) {
    auto pivot = *(last - 1);
    Iterator i = first;
    for (Iterator j = first; j < last - 1; ++j) {
        if (comp(*j, pivot)) {
            std::iter_swap(i, j);
            ++i;
        }
    }
    std::iter_swap(i, last - 1);
    return i;
}

// Introsort 主函数
template<typename Iterator, typename Compare>
void introsort_helper(Iterator first, Iterator last, int depth_limit, Compare comp) {
    while (last - first > 16) { // 使用插入排序的阈值
        if (depth_limit == 0) {
            // 切换到堆排序
            std::make_heap(first, last, comp);
            std::sort_heap(first, last, comp);
            return;
        }
        --depth_limit;
        Iterator pivot = partition(first, last, comp);
        introsort_helper(pivot, last, depth_limit, comp);
        last = pivot;
    }
    // 使用插入排序
    std::insertion_sort(first, last, comp);
}

// std::sort 的简化实现
template<typename Iterator, typename Compare>
void introsort(Iterator first, Iterator last, Compare comp) {
    int depth_limit = 2 * log(last - first);
    introsort_helper(first, last, depth_limit, comp);
}

int main() {
    std::vector<int> data = {10, 7, 8, 9, 1, 5};
    std::sort(data.begin(), data.end()); // 实际调用的是标准库的 std::sort
    for(auto num : data)
        std::cout << num << " ";
    return 0;
}

C++ 中的std::stable_sort函数

std::stable_sort函数通常由归并排序实现，标准库对归并排序有多种优化，以提高缓存局部性和减少内存分配次数，如使用自底向上的归并排序和内省策略来选择合适的排序方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <vector>
#include <iostream>

// 合并两个有序子数组
template<typename T, typename Compare>
void merge(std::vector<T>& data, int left, int mid, int right, Compare comp) {
    int n1 = mid - left + 1;
    int n2 = right - mid;

    // 创建临时数组
    std::vector<T> L(n1);
    std::vector<T> R(n2);

    for(int i = 0; i < n1; ++i)
        L[i] = data[left + i];
    for(int j = 0; j < n2; ++j)
        R[j] = data[mid + 1 + j];

    // 合并临时数组回原数组
    int i = 0, j = 0, k = left;
    while(i < n1 && j < n2) {
        if(comp(L[i], R[j])) {
            data[k++] = L[i++];
        }
        else {
            data[k++] = R[j++];
        }
    }

    // 复制剩余元素
    while(i < n1)
        data[k++] = L[i++];
    while(j < n2)
        data[k++] = R[j++];
}

// 归并排序的主函数
template<typename T, typename Compare>
void merge_sort(std::vector<T>& data, int left, int right, Compare comp) {
    if(left < right) {
        int mid = left + (right - left) / 2;
        merge_sort(data, left, mid, comp);
        merge_sort(data, mid + 1, right, comp);
        merge(data, left, mid, right, comp);
    }
}

// std::stable_sort 的简化实现
template<typename T, typename Compare>
void stable_sort_impl(std::vector<T>& data, Compare comp) {
    merge_sort(data, 0, data.size() - 1, comp);
}

int main() {
    std::vector<int> data = {10, 7, 8, 9, 1, 5};
    std::stable_sort(data.begin(), data.end()); // 实际调用的是标准库的 std::stable_sort
    for(auto num : data)
        std::cout << num << " ";
    return 0;
}
排序算法
https://kevin346-sc.github.io/2024/10/04/排序算法/
作者
Kevin Huang
发布于
2024年10月4日
许可协议