template

并查集DisjointSet

并查集中每个强连通分量视为一个集合，强连通分量中任意两点均可达

并查集的两个基本操作

  • Find：查找元素所属集合
  • Union：合并两个子集为一个新的集合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Disjointset{
	private: 
		vector<int> fa;
    	Disjointset(int max_size): fa(vector<int>(max_size))
        {
            // 初始化fa数组
            iota(fa.begin(), fa.end(), 0);
        }
	public:
        int Find(int x)
        {
            if(fa[x] == x) // 自己就是根结点
                return x;
            else //继续查找父结点，直到根结点
            {
                int parent = Find(fa[x]);
                return parent;
            }
            // 三目运算符写法
            // return fa[x] == x ? x : Find(fa[x]);
        }

        void Union(int a, int b)
        {
            int pa_a = Find(a);
            int pa_b = Find(b);
            if(pa_a == pa_b) // 同属一个集合中，无需合并
                return;
            fa[pa_a] = pa_b;
            // 也可以无需判断，直接写成 fa[pa_a] = pa_b;
        }
};

这样子，在树高较高的情况下（链表），find的复杂度可以达到O(n)，可以通过秩或者路径压缩的方法来减小复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
// 秩，代表树的高度
// 当秩为a 与 秩为b 的两个子集合并时，将秩较小的合并到秩较大的集合上；若相等，则任意合并，秩+1
class Disjointset{
	private: 
		vector<int> fa;
		vector<int> rank; // 秩
    	Disjointset(int max_size): fa(vector<int>(max_size), rank(vector<int>(max_size, 0)))
        {
            // 初始化fa数组
            iota(fa.begin(), fa.end(), 0);
        }
	public:
        int Find(int x)
        {
            if(fa[x] == x) // 自己就是根结点
                return x;
            else //继续查找父结点，直到根结点
            {
                int parent = Find(fa[x]);
                return parent;
            }
            // 三目运算符写法
            // return fa[x] == x ? x : Find(fa[x]);
        }

        void Union(int a, int b)
        {
            int pa_a = Find(a);
            int pa_b = Find(b);
            if(rank[pa_a] > rank[pa_b])
            {
            	fa[pa_b] = pa_a;
            }
            else
            {
            	fa[pa_a] = pa_b;
            	if(rank[pa_a] == rank[pa_b])
            		rank[pa_b]++;
            }
        }
};


// 路径压缩
class Disjointset{
	private: 
		vector<int> fa;
    	Disjointset(int max_size): fa(vector<int>(max_size))
        {
            // 初始化fa数组
            iota(fa.begin(), fa.end(), 0);
        }
	public:
        int Find(int x)
        {
            // 三目运算符写法
            // return fa[x] == x ? x : Find(fa[x]);
            // 在向上查找根结点时，每个孙子结点都变为子结点，减小树高
            return fa[x] == x ? x : fa[x] = Find(fa[x]);
        }

        void Union(int a, int b)
        {
            int pa_a = Find(a);
            int pa_b = Find(b);
            if(pa_a == pa_b) // 同属一个集合中，无需合并
                return;
            fa[pa_a] = pa_b;
            // 也可以无需判断，直接写成 fa[pa_a] = pa_b;
        }
};

时间复杂度：O(n+m×α(m))，其中 n 是图中的顶点数，m 是图中边的数目，α 是反阿克曼函数，在n非常大的时候，α(n) < 5。并查集的初始化需要 O(n)的时间，然后遍历 m 条边并执行 m 次合并操作，最后对 source 和 destination 执行一次查询操作，查询与合并的单次操作时间复杂度是 O(α(m))，因此合并与查询的时间复杂度是 O(m×α(m))，总时间复杂度是 O(n+m×α(m))

2316. 统计无向图中无法互相到达点对数

附加数组信息，保存节点数信息

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Disjointset{
    private:
        vector<int> fa;
        vector<int> rank;
    public:
        Disjointset(int n): fa(vector<int>(n)), rank(n, 1)
        {
            iota(fa.begin(), fa.end(), 0);
        }

        int find(int x)
        {
            if(x == fa[x])
                return x;
            else
            {
                fa[x] = find(fa[x]);
                return fa[x];
            }
        }

        void Union(int x, int y)
        {
            int pa_a = find(x);
            int pa_b = find(y);

            if(pa_a == pa_b)
                return;
            if(rank[pa_a] > rank[pa_b])
            {
                fa[pa_b] = pa_a;
                rank[pa_a] += rank[pa_b];
            }
            else
            {
                fa[pa_a] = pa_b;
                rank[pa_b] += rank[pa_a];
            }   
        }

        int get(int x)
        {
            return rank[x];
        }
};
class Solution {
public:
    long long countPairs(int n, vector<vector<int>>& edges) {
        Disjointset disjointset(n);
        for(const auto & edge : edges)
        {
            disjointset.Union(edge[0], edge[1]);
        }
        long long res = 0;
        for(int i = 0; i < n; i++)
        {
            res += n - disjointset.get(disjointset.find(i));
        }
        return res / 2;
    }
};

字典树 Trie

字典树（trie），是一种特别的树，用来高效查找和存储大量有字符串，并能快速查找单词前缀，其中，每个节点都存储了指向子节点的指针数组，以及一个bool字段，用来判断当前字符是否为字符串的结尾，所谓的字符并没有实际储存，而是通过比如储存只有小写字母或者只有大写字母的字符串时，初始化指针数组的长度为26，当该节点的数组不为nullptr，即为有该序号对应的字符存在，指针指向下一个字符，同样在读取下下一个字符时，也能按照同样的方法找到，当某个节点的bool字段为true时，证明已经有一个单词读取完毕，但也可能还有其他单词有着相同的前缀。字典树实现如下

208. 实现 Trie (前缀树)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Trie {
public:
    vector<Trie*> tr;
    bool isEnd;
    Trie() {
        tr.resize(26);
        isEnd = false;
    }
    
    void insert(string word) {
        Trie* cur = this;
        for(const auto& c : word)
        {
            if(!cur->tr[c - 'a'])
                cur->tr[c - 'a'] = new Trie();
            cur = cur->tr[c - 'a'];
        }
        cur->isEnd = true;
    }
    
    bool search(string word) {
        Trie* cur = this;
        for(const auto& c : word)
        {
            if(!cur->tr[c - 'a'])
                return false;
            cur = cur->tr[c - 'a'];
        }
        return cur->isEnd == true;
    }
    
    bool startsWith(string prefix) {
        Trie* cur = this;
        for(const auto& c : prefix)
        {
            if(!cur->tr[c - 'a'])
                return false;
            cur = cur->tr[c - 'a'];
        }
        return true;
    }
};

字符匹配算法

字符串匹配问题，即在给定的文本串string中寻找有无模式串pattern的存在，最朴素的解决方法是用O(mn)的复杂度，依次遍历string中是否有完整的pattern存在，也称做暴力匹配，其他常见算法还有Knuth-Morris-Pratt 算法、Boyer-Moore 算法、Sunday 算法等。

Sunday算法

Sunday算法核心思想在于在匹配失败时，跳过尽可能多的字符以达到更高的效率，因此需要借助一个move数组，记录模式串匹配失败时需要移动的距离，move数组的建立规则:当遇到匹配失败情况时，如果该字符不存在于模式串中，需要将模式串向右 移动模式串长度 + 1位；如果该字符在模式串中存在，则将模式串向右移动 模式串长度 - 该字符在模式串中最右边的位置 + 1位，例如，在文本串substring searching中匹配模式串search过程如下，先对齐起始位置，发现字符i不存在于模式串中

![image-20240825120700691](C:\Users\kevin\AppData\Roaming\Typora\typora-user-images\image-20240825120700691.png

那么需要将模式串向右移动7位，此时匹配失败，指向字符r，存在于模式串中， 那么只需要将模式串向右移动3位，然后就匹配成功了

![image-20240825120736268](C:\Users\kevin\AppData\Roaming\Typora\typora-user-images\image-20240825120736268.png

算法实现如下，找出字符串中第一个匹配项的下标

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int strStr(string haystack, string needle) {
        int m = haystack.size(), n = needle.size();
        unordered_map<int, int> umap;
        for(int i = n - 1; i >= 0; i--)
        {
        	if(umap.find(needle[i]) != umap.end())
        		continue;
        	umap[needle[i]] = n - i;
        }
        int i = 0;
        while(i <= m - n)
        {
			if(haystack.substr(i, n) == needle)
				return i;
			if(i + n > m)
				return -1;
			if(umap.find(haystack[i + n]) != umap.end())
			{
                i += umap[haystack[i + n]];
			}
			else
			{
				i += n + 1;
			}
		}
        return -1;
    }
};

Sunday算法平均时间复杂度为O(n)，但最坏情况时间复杂度可能达到O(mn)，特别是在文本串与模式串结构复杂或匹配不成功时。

KMP算法

KMP算法性能最优，能达到O(m + n)的时间复杂度，其核心在于next数组，next数组保存的是pattern模式串的最长公共前后缀长度，例如abcabf所对应的next数组[0, 0, 0, 1, 2, 0]，前缀的应用在于匹配串，后缀的应用在于原字符串，那么我们就可以通过最长公共前后缀，也就是next数组，来帮助我们在匹配失败时快速找到下一个应该匹配的位置。例如，如果要在string='aabaabaaf'中，寻找pattern='aabaaf'，pattern对应的next数组是[0, 1, 0, 2, 0]，如果当前匹配的string[i] == pattern[j]，跟暴力匹配一样，直接i++,j++进入下一轮匹配

image-20240824110732810

但在匹配到string[i] != pattern[j]时，朴素算法将j回退到0，i也要回退到之前匹配的下一个位置，也就是i=1，j=0重新进行匹配，但这样明显不合理，因为我们已经知道这样匹配最后还是回到i的位置，而j会遍历到j=2的位置，也就是下图所示

image-20240824111757792

而这就能够与next数组扯上了关系，在pattern匹配失败时，i不需要改变位置，只需要根据next[j - 1]的位置来调整j，再接着匹配string[i]是否等于pattern[j]。直观上讲，在匹配失败时，i=5,j=5,也就是string.substr(0, 5) == pattern.substr(0, 5),那么下一个还能匹配成功的位置自然就是最长公共前后缀了，因此我们可以先计算出next数组，再利用next数组在我们匹配失败时快速调整新的匹配位置从而降低复杂度

那么应该如何来求next数组呢，最简单的办法自然也是O(n^2)，但还可以有O(n)的方法，那就是利用已计算出来的next数组，为了方便计算，next数组长度设为n+1，并令next[0] = -1，这样在调整j的位置时可以直接将j = next[j]，也就是把next数组整体向右移了一位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void get_next(vector<int>& next, string p)
{
	int n = p.size();
	next.assign(n + 1, 0);
	next[0] = -1;
	int j = -1 , i = 0;
	while(i < n)
	{
		if(j == -1 || p[i] == p[j])
		{
			i++, j++;
			next[i] = j;
		}
		else
		{
			j = next[j];
		}
	}
}

在计算next数组过程中，用i记录遍历过程， j表示最大公共前后缀的长度

next[i] 表示pattern[0,…,i - 1]的字符串最大公共前后缀长度

next[i - 1] 表示pattern[0,…,i - 2]的字符串最大公共前后缀长度

当遍历到pattern[i]时，从next[i]可知，当前pattern[0,…,i - 1]中长度为next[i]的前缀等于其长度为next[i]的后缀，也就是图中黄色区域，

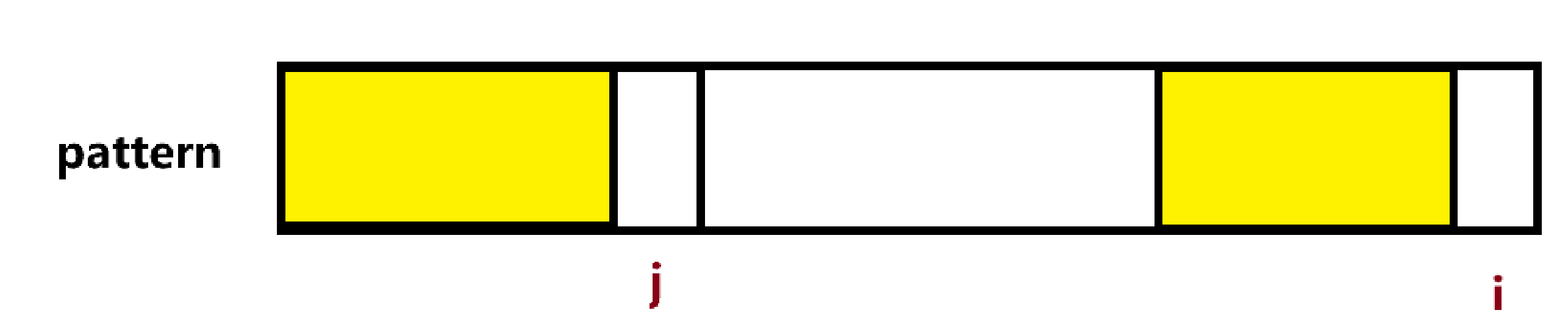
image-20240824152610683

那么接下来，就看pattern[i]是否与pattern[j]想等，如果相等，那么next[i+1]的最大公共前缀和更新为pattern[0,…,i]，最大公共前缀和长度更新为j+1;

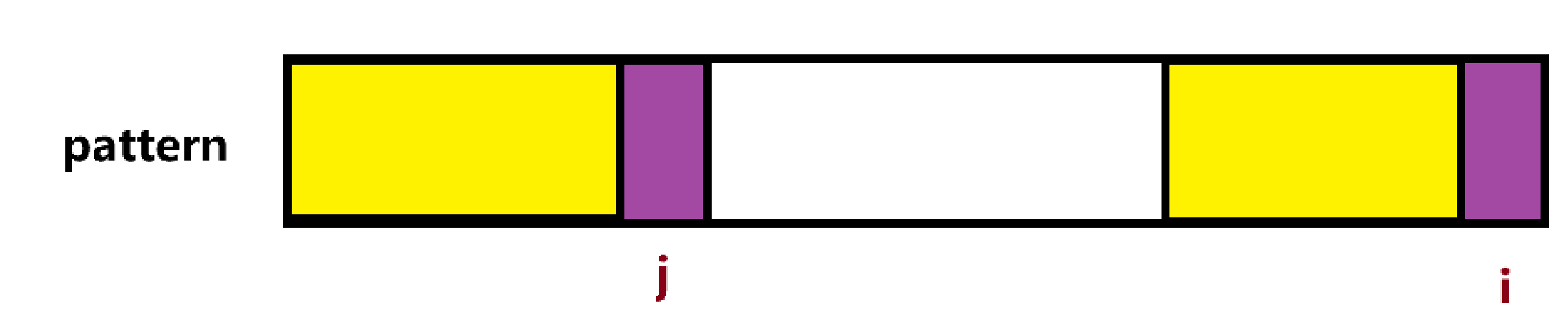
image-20240824152516181

如果不相等，就需要寻找新的最大公共前后缀位置，而新的公共前后缀必然更小，就比如图中的红色区域

image-20240824152940102

又因为pattern[0,…,i - 1]的前后缀相同，也就是黄色区域相同，所以新的公共前后缀其实就是原来公共前后缀的公共前后缀，如图中红色区域，代码中体现就是j=next[j]

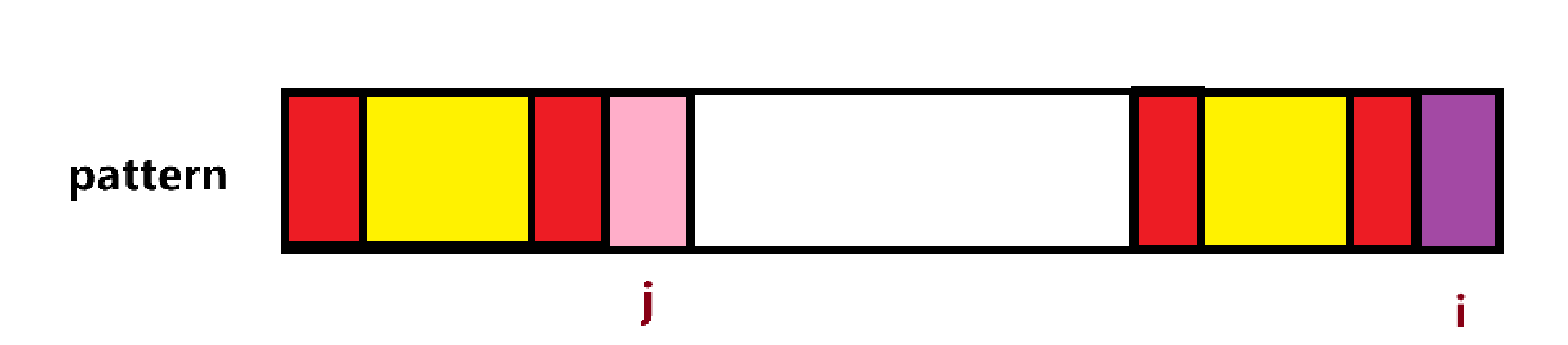
image-20240824153408193

在得到next数组后，就可以在一次遍历中匹配模式串

例如，找出字符串中第一个匹配项的下标

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    void get_next(vector<int>& next, string p)
    {
        int n = p.size();
        next.assign(n + 1, 0);
        next[0] = -1;
        int j = -1 , i = 0;
        while(i < n)
        {
            if(j == -1 || p[i] == p[j])
            {
                i++, j++;
                next[i] = j;
            }
            else
            {
                j = next[j];
            }
        }
    }
    int strStr(string haystack, string needle) {
        int m = haystack.size(), n = needle.size();
        vector<int> next(n + 1, 0);
        get_next(next, needle);
        int j = 0, i = 0;
        while(i < m && j < n)
        {
            if(j == -1 || haystack[i] == needle[j])
            {
                i++, j++;
            }
            else
            {
                j = next[j];
            }
        }
        if(j == n)
            return i - j;
        return -1;
    }
};

综上，Sunday算法适用在较短文本、单词分布均匀的字符串匹配中，而KMP算法更适用在复杂的长文本中，同时KMP有更稳定的性能保持在O(m + n)的时间复杂度

template
https://kevin346-sc.github.io/2023/11/19/template/
作者
Kevin Huang
发布于
2023年11月19日
许可协议